ん？このサイトはいつから料理サイトになったんだ？
さて、本日メニュー・・・もとい、
本日のテーマは二重積分です。二を省略して、重積分と呼ばれることが多いですよ。
【積分】【重積分】【三重積分】
この３つの違いがよくわからない人って多いと思うんですよ。
ここではわかりやすく？料理の切り方に例えてご紹介します。
【積分】【重積分】【三重積分】はイラストを見たら一発で区別できるぞ！
重積分とは
さて、積分は高校のときに習いましたよね。面積を表すのに使われ、たくさん計算をしてきたのではないでしょうか。
一方、重積分はどんなときに使うかというと・・・
底面が平らな立体の体積
を表すときに使われます。
※底面が平らでないときは、ぶった切れば底面が平らな立体２つにわけて考えることができる。
例 \(\iint_D xy dxdy\) , \(D=\){\((x,y)|x^2 \leq y \leq 2x\)} を計算せよ
のようにインテグラルが２つついているものが重積分です。このように体積の計算をするために使われます。
う～ん。立体の体積か。でも三重積分もそんな感じじゃない？
・・・・・・そうだな。じゃあまずは、イメージで捉えてみようか！
積分は千切り、重積分は拍子木切り、三重積分はさいの目切りのイメージ
「いや、そもそもその切り方がわかんないから！」って言われると思うので、イラストを見てイメージを掴んでください。
左から、キャベツの千切り 大根の拍子木切り 大根のさいの目切り です。
積分
積分を使って曲線で囲まれた面積を求めるとき ⇒ x方向に細かくして、帯に分けて考える
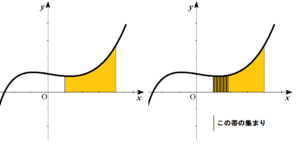
（面積を細長い長方形の集まりと考える）：キャベツの千切り
重積分
重積分を使って立体の体積を求めるとき ⇒ x方向y方向に細かくして立体の細長い柱に分けて考える
（体積を細長い直方体の集まりと考える）：大根の拍子木切り
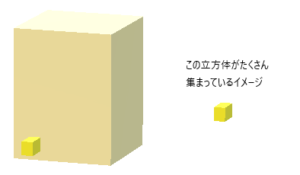
三重積分
三重積分を使って立体の体積を求めるとき ⇒ 立方の細長い柱をさらに細かくして立方体に分けて考える
（体積を立方体の集まりと考える）；大根のさいの目切り
それぞれちゃんと違いがあるんだ！なんかイメージは湧いたかも！
重積分の数学的な定義
１変数関数 \(y=f(x)\) の定積分 \(\int_a^b f(x)dx\) は区間 \([a,b]\) 上の面積を求める際に使われます。これが積分です。
一方で、２変数関数 \(z=f(x,y)\) の積分
\(\iint_D f(x,y)dxdy\)
は平面の領域 \(D\) 上の体積を求める際に使われます。これが重積分です。
重積分には重要な定理がいくつかあるので、確認しておきましょう。
\(f(x,y) , g(x,y)\) が \(D\) で積分可能であるとき以下が成り立つ。 (ただし \(α,β\) は定数とする)
(1) \(\iint_D \){\(αf(x,y)+βg(x,y)\)}\(dxdy = α\iint_D f(x,y)dxdy + β\iint_D g(x,y)dxdy\) (2) \(D\) で \(f(x,y) \leq g(x,y)\) ならば \(\iint_D f(x,y)dxdy \leq \iint_D g(x,y)dxdy\) (3) \(f(x,y)g(x,y)\) は \(D\) で積分可能である\(D = [a,b] × [c,d] \)のとき
\(\iint_D f(x,y)dxdy = \int_a^b (\int_c^d f(x,y)dy)dx = \int_c^d (\int_a^b f(x,y)dx)dy\)
いかがでしたでしょうか。
具体的な計算はまた次の機会にまわします。今回は【積分】【重積分】【三重積分】の区別が出来ればクリアです！
イメージで「面積・体積を細かくして計算を行う」ということがおわかりいただければと思います。
動画解説はこちら
