ヤコビアンっていつ使うんだろう・・・
さて、今回のテーマは「極座標変換で積分計算をする方法」です。
ヤコビアンについては前回勉強をしましたね。ここでは、実際の計算例をみて勉強を進めてみましょう。
ヤコビアンの定義についてはこちらのページをみてください：ヤコビアンとは？
まずは基礎をしっかり確認してから例題をみてみよう！
例題１
重積分
\(\iint_D 2dxdy\) を求めよ。
まず、この直交座標表示を極座標表示に変えると、
\(x=rcosθ,y=rsinθ\)
を適応させることになる。ここで、極座標変換のヤコビアンは
\(|\frac{∂(x,y)}{∂(r,θ)}|=\begin{vmatrix} cosθ& -rsinθ\\sinθ&rcosθ\end{vmatrix}=r\)
と表されるので、領域 \(D\) を \((r,θ)\) で表すと、
\(\iint_D 2dxdy =\iint_E 2rdrdθ\)となる。よって、
\(\iint_D 2dxdy =\int_0^{\frac{\pi}{2}} \int_0^1 2rdrdθ \)
\(= \int_0^{\frac{\pi}{2}} [r^2]_0^1 dθ\)
\(=\int_0^\frac{\pi}{2} dθ\)
\(=\frac{\pi}{2}\)
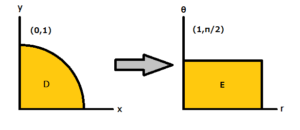
この計算は上図のように、曲線を直線に変換して計算しているイメージだ
例題２
多重積分
\(I=\iint_D (x^2 +y^2)dxdy , D=\){ \((x,y)|x^2+y^2 \leq a^2\)} \((a>0)\)を求めよ。
まず、この直交座標表示を極座標表示に変えると、
\(x=rcosθ,y=rsinθ\)
を適応させることになる。ここで、極座標変換のヤコビアンは
\(|\frac{∂(x,y)}{∂(r,θ)}|=\begin{vmatrix} cosθ& -rsinθ\\sinθ&rcosθ\end{vmatrix}=r\)
と表されるので、領域 \(D\) を \((r,θ)\) で表すと、
\(E=\){\((r,θ)|0 \leq r \leq a , 0 \leq θ \leq 2\pi\)} となる。よって、
\(\iint_D (x^2 +y^2)dxdy = \iint_E ((rcosθ)^2 + (rsinθ)^2)|\frac{∂(x,y)}{∂(r,θ)}|drdθ\)
\(= \iint_E r^3 drdθ \)
\(= \int_0^{2\pi} dθ \int_0^a r^3 dr\)
\(= (\int_0^{2\pi} dθ)(\int_0^a r^3 dr )\)
\(=[θ]_0^{2\pi} × [\frac{r^4}{4}]_0^a \)
\(=\frac{\pi a^4}{2}\)
多重積分の極座標変換において \(dxdy=rdrdθ\) である
これはよく使うから、その都度いちいち計算をするのではなく、公式として暗記をしておいたほうがいいぞ！
確かに・・・結構毎回出てくるし、これを覚えておいたほうがいいかも
ヤコビアンについてはあまり動画がないのですが、この動画は図形的表現が非常にわかりやすいです。
言葉はわからなくても、数式と図で理解できると思います。数学は世界共通語！！
