ハイパボリックサインって言葉を聞いたことはあるけど、実際明確にハイパボリックサインが何を表すかって聞かれたら結構困りませんか？
なんとなくきっちりとした理解から避けてきた人も多いかもしれませんが、一緒に頑張って理解していきましょう。
ハイパボリックサインって言葉どういう意味?
ハイパボリックと言うのは双曲線という意味で、サインの意味は、標準系の双曲線関数を媒介変数表示した時に現れるy座標の式で在るためです。
これらの意味を組み合わせ合わせて、ハイパボリックサインと言う名前になっております。
ちなみに、略す時はシャインと言われる事が、多いようです。
2.sinh xのxって何?角度?
ハイパボリックサインは面積で定義される
$$標準形の双曲線上の点 A と x 軸上の点 B (1, 0) を取り、$$
$$線分 AO、BO と双曲線の囲む領域の面積が \frac{ θ } { 2 } であるとき、$$
$$A の y 座標を \sinh θ として、双曲線関数 \sinh が定義される。$$
$$繰り返しますが、面積が\frac{ θ } { 2 }の時のθがcos h θ のθに対応します。\\点 A と原点とのなす角ではありません注意しましょう$$
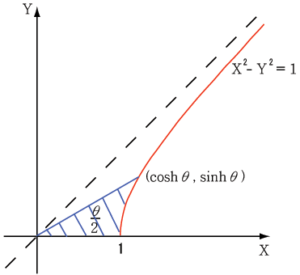
出展 Wikipedia
同条件で、sin θ を定義した場合 sin θ は単位円で定義される為
$$弧度法で、円の面積は、S={\frac {1}{2}}\thetaであるから。 $$
sin θ のθが点Aと原点のなす角で有ることは、変わりはない。
3.ハイパボリックサインの軌跡
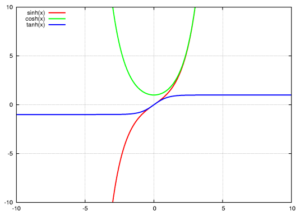
出展 Wikipedia
軌跡の特徴として、単調増加で原点対称の奇関数です。
4.微分して見よう
\[y = \sinh x = \frac{ e^{x} – e^{-x} } { 2 } \]
で、与えられ
$$ (sinh x）^{\prime} = (\frac{ e^{x} – e^{-x} } { 2 }）^{\prime} = \frac{ e^{x} + e^{-x} } { 2 } =\cosh x$$
最後に出てきた、coshは、ハイパボリックコサインと呼ばれています。
まとめ
如何でしたか？微分はとても簡単だったと思います。定義が面積によって行われることに注意してください。
最後に先生、締めの挨拶お願いします
任せろ!!あれ?風邪かなぁ…ふぁふぁ、ハッシャイーン
ハイパボリックコサインと双曲線関数の記事にいる先生のくしゃみはどうやら違う用です
お見舞いに行ってやって下さい
微分ミスってるで
内容修正いたしました。
今後も何かありましたらご連絡くださいませ。
微分のところ間違ってます
Cosh だと e^(-x)の係数は、+(1/2)のはず