二次元をようやく理解したと思ったら、三次元来ちゃったよ・・・
ということで、今回のテーマは三次元の直交座標と極座標についてです。なんとなく存在は知っている人もいるかもしれませんが、ここでは、その定義と変換方法をご紹介します。
「どうやって変換するの？」と思われる方もいると思うので、その方法をご紹介します。
三次元の直交座標とは
三次元直交座標は \(P(x,y,z)\) で点の位置を表す方法 である
これは高校のときに勉強しましたよね。平面的にみていた二次元と違って、高さ \(z\) がでた分、座標は３つになります。
しかし、考え方としては二次元のときとさほど変わりません。
三次元極座標とは
三次元極座標は \(P(r,θ,φ)\) で点の位置を表す方法である
\(r\) ：極\(O\)から点\(P\)までの距離
\(θ\)：\(z\) 軸の性の向きと \(OP\) のなす角
\(φ\)：\(x\)軸の性の向きと\(OQ\) のなす角
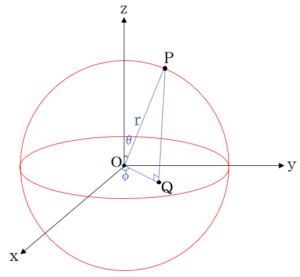
直交座標系と極座標系の変換について
さて、ひき続きそれぞれの方向からの変換の公式をみてみましょう。
極座標 \((r,θ,φ)\) から直交座標 \((x,y,z)\) への変換
\(x=rsinθcosφ\) ，\(y=rsinθsinφ\) ，\(z=rcosθ\)
直交座標 \((x,y,z)\) から極座標 \((r,θ,φ)\) への変換
\(r=\sqrt{x^2+y^2+z^2}\) ，\(θ=Arccos\frac{z}{\sqrt{x^2+y^2+z^2}}\) ，\(φ=Arccos\frac{x}{\sqrt{x^2+y^2}}\)
Arccos（アークサイン）がわからない人は以前紹介したページに戻ろう！
変換については理解できたでしょうか。
三重積分の活用法
さて、ここで三重積分の話もしておきます。
実は、三重積分は、重積分を先に行い、後で（１重）積分を行っているだけなのです。
なるほど、そういう仕組みになっているのかぁ
例を見てみましょう。
\(V = \){\((x,y,z) | x^2+y^2+z^2 \leq a^2 , 0\leq x , 0\leq y , 0\leq z\)} \((0<a)\)
とするとき, 次の三重積分を計算せよ。
\(\iiint_V x dxdydz\)
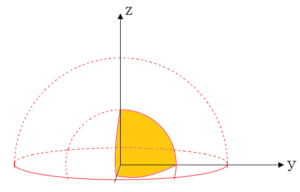
ここで、\(V\) は \(V = \){\((x,y,z) | 0 \leq x \leq a , y^2+z^2 \leq a^2 – x^2 , 0 \leq y , 0 \leq z \)}と表される。
そこで、 \(D_x =\){\(y,z) | y^2+z^2 \leq a^2 – x^2 , 0\leq y, 0 \leq z\)}と置くと、
\(\iiint_V xdxdydz = \int_0^a dx \iint_{D_x} xdydz\)
ここで、\(\iint_{D_x} dydz\) は半径 \(\sqrt{a^2 – x^2}\) の円板の面積の\(\frac{1}{4}\) であるから、
\(\iint_{D_x} xdydz = x \cdot \frac{\pi (a^2 – x^2 )}{4}\)
である。よって、
\(\iint_V xdxdydz = \frac{\pi}{4} \int_0^a (a^2 x – x^3)dx = \frac{\pi}{4}[\frac{1}{2}a^2 x^2-\frac{1}{4}x^4]_0^a = \frac{\pi}{16} a^4\)
となるわけです。
やっぱりこの分野の解説はこの人に任せましょう
