$$\newcommand{\diff}{\mathrm{d}}$$
複素フーリエ級数展開を導出しましたが、まだ、心もとないという人がほとんどのように思います。複素フーリエ級数展開がとてもシンプルな形になるのですが、「だからそれがどうしたの？」と一斉に突っ込まれるのではないかと思われます。
ここでは大変有名な公式の一つであるオイラーの公式から実数のフーリエ級数展開(実フーリエ級数展開)が複素フーリエ級数へと導かれたその意味をたしかなものにするために例題で確認してゆきたいと思います。
例題1.矩形波
まず、実フーリエ級数展開でも例題として取り上げた矩形波で複素フーリエ級数展開がどうなるのか見てみたいと思います。複素フーリエ級数展開は、周期2Lのとき
$$f(x) = \sum_{n=-\infty}^{\infty}c_n\mathrm{e}^{i\frac{2\pi}{L}nx}$$
$$c_n = \frac{1}{2\pi}\int_{0}^{L} f(x)\mathrm{e}^{-i\frac{2\pi}{L}nx} \diff x$$
でしたね。それでは矩形波の複素フーリエ級数展開を例題で見てゆきましょう。
$$f(x) = \left\{\begin{array}{1}1 &(\pi \leq x < 0) \\ -1 &(0 \leq x < \pi)\end{array}\right.\tag{1}$$
(1)をグラフにすると
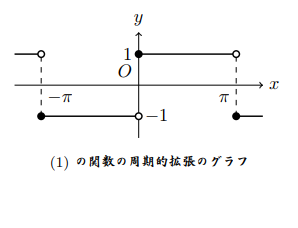
です。まず、(1)は、
$$\begin{align*}c_0 & = \frac{1}{2\pi}\int_{-\pi}^{\pi} f(x) \diff x \\ & = \frac{1}{2\pi} \left\{ \int_{-\pi}^{0} \diff x + \int_{0}^{\pi} 1 \diff x \right\} \\ & = \frac{1}{2\pi}\left\{[-x]^0_{-\pi} + [x]^{\pi}_0\right\} \\ & = 0\end{align*}$$
次に$$n \neq 0$$のときは次のとおりです。
$$\begin{align*}c_n & = \frac{1}{2\pi}\int_{-\pi}^{\pi}f(x)\mathrm{e}^{-i n x} \diff x\\ & = \frac{1}{2\pi}\left\{\int_{-\pi}^{0} (\mathrm{-e}^{-inx}) \diff x+ \int_{0}^{\pi}\mathrm{e}^{-inx} \diff x\right\} \\ & = \frac{1}{2\pi}\left\{\bigg[\frac{1}{in}\mathrm{e}^{-inx}\bigg]^{-\pi}_{0} + \bigg[-\frac{1}{in}\mathrm{e}^{-nx}\bigg]^{\pi}_0\right\} \\ & = \frac{1}{2\pi}\left\{-\frac{i}{n}(1 – \mathrm{e}^{inx} )+ \frac{i}{n}(\mathrm{e}^{-inx} – 1)\right\} \\ & = \frac{1}{2\pi n}(\mathrm{e}^{i\pi n} + \mathrm{e}^{-i\pi n}) – \frac{i}{\pi n}\end{align*}$$
ここでオイラーの公式の登場です。
整数kに対して $$\mathrm{e}^{i\pi k} = \cos(\pi k) + i\sin(\pi k) = (-1)^k$$ が成り立ちます。
上記の式にオイラーの公式を当てはめると
$$\begin{align*} & = \frac{i}{2\pi n}\times 2\cos \pi n – \frac{i}{\pi n}\end{align*}$$
以上より、複素フーリエ級数展開は
$$\begin{align*}f(x) \sim \sum_{\substack{k = -\infty} \\ {k \neq 0}}^{\infty}\frac{i}{\pi k}(\cos \pi k – 1)\mathrm{e}^{ikx}\end{align*}$$
例題2.指数関数
例2として$$f(x) = \mathrm{e}^{x} (-\pi < x < \pi)$$の複素フーリエ級数展開を見てみましょう。グラフにすると下記のようになります。
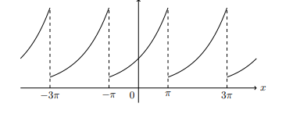
複素フーリエ級数展開から
$$\begin{align*}c_n & = \frac{1}{2\pi}\int_{-\pi}^{\pi}f(x)\mathrm{e}^{-inx} \diff x \\ & = \frac{1}{2\pi}\int_{-\pi}^{\pi} \mathrm{e}^{x} \mathrm{e}^{-inx} \diff x \\ & = \frac{1}{2\pi}\int_{-\pi}^{\pi} \mathrm{e}^{x – inx} \diff x \\ & = \frac{1}{2\pi}\left[\frac{1}{1 – in}\mathrm{e}^{x – inx}\right]_{-\pi}^{\pi} \\ & = \frac{1}{2\pi}・\frac{1}{1 – in}(\mathrm{e}^{\pi- in\pi} – \mathrm{e}^{-\pi + in\pi}) \\ & = \frac{(-1)^n}{2\pi(1 – in)}(\mathrm{e}^{\pi} – \mathrm{e}^{-\pi})\end{align*}$$
ここで、
$$\frac{1}{1 – in} = \frac{1 + in}{(1 + in)(1 – in)} = \frac{1 + in}{1 + n^2} ,\,\mathrm{e}^{\pi} – \mathrm{e}^{-\pi} = 2 \sinh \pi$$
以上のことから$$c_n$$が求まります。
$$c_n = \frac{\sinh \pi}{\pi}\frac{1 + in}{1 – n^2}(-1)^n$$
を得ます。このことからfの複素フーリエ級数は下記のようになります。
$$f(x) \sim \frac{\sinh \pi}{\pi}\sum_{n=-\infty}^{\infty}(-1)^n\frac{1 + in}{1 + n^2}\mathrm{e}^{inx}$$
先生、なんだかキツネにつままれたみたいです。
ケイスケくん、複素フーリエ級数の計算はね、オイラーの公式を上手に使いながら、ひたすら三角関数と虚数の計算ばかりで、$$c_n$$が求められれば後は積分するだけなんだよ。何も難しいことはしていないんだ。
慣れの問題かな、先生。
そうだね。これが大学の数学というものだからね。
まとめ
複素フーリエ級数展開の例題を解くことで複素フーリエ級数の理解が深まればいいのですが、どうでしょうか。今回はひたすらに計算することばかりでしたが、複素フーリエ級数はそんなに難しいことはなく、三角関数と虚数、そしてオイラーの公式さえ頭に入っていれば、必ず解けます。
フーリエ級数でつまづいて、大学四年間数学があやふやなまま過ごしてしまい、結局フーリエ級数が何なのかわからずじまいという人も少なくありません。フーリエ級数はどんな関数も三角関数で表せるということをいっているに過ぎないのです。複素フーリエ級数ではなんといってもオイラーの公式がものをいうので、まだ、うろ覚えという人は今日覚えてください。
