これまでフーリエ級数展開、偶関数、奇関数、関数の内積、そして複素フーリエ級数など説明してきましたが、だからフーリエ級数はなに?と感じている人も多いのかも知れません。そこで、フーリエ級数、つまり、三角関数の和でたいていの周期関数が解析できてしまうということを例題で示そうと思います。
フーリエ級数の求め方を例題で確認してみよう!ということです。簡単な周期関数の例でもって実際にフーリエは級数はどうなるのかを見てゆきたいと思います。
三角関数は直交関数系
例を見る前に、三角関数が直交関数系ということに関して見ておきます。
三角関数が直交関数系ということはわかったでしょう。
例1.矩形波
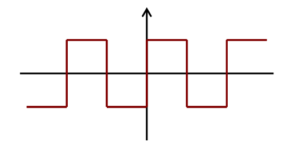
上記のような矩形波は、たとえば次のような関数で表されます。
$$f(t) = \left \{ \begin{array}{1} -1 & (\pi ≦ t < 0) \\ 1 & (0 ≦ t < \pi)\end{array} \right., f(t + 2\pi) = f(t)$$
これをフーリエ級数で表してみましょう。まず、フーリエ級数展開は、
| $$f(t) = a_0 + \sum_{n =1}^{\infty} ( a_ncos(nt) + b_nsin(nt))$$ |
でしたね。これからフーリエ係数を求めるのですが、フーリエ係数を覚えていますか? フーリエ係数は$$a_nとb_n$$のことでしたよね。この例題では$$区間[-\pi, \pi]$$ですので、フーリエ係数はそれぞれ次のように導かれます。それでは、まず、三角関数は直交関数系ということから、上記のフーリエ級数展開の両辺を積分するとa0項のみが残ります。
| $$\int_{-\pi}^{\pi} f(t) = \int_{-\pi}^{\pi} a_0 dt = 2\pi a_0$$ |
同じように三角関数の直交関数系で求めたフーリエ級数の両辺にcos(nt)をかけて積分するとamの項のみが残り、両辺にsin(nt)をかければbmのみが残ります。
| $$\int_{-\pi}^{\pi} f(t) cos(nt) dt = \int_{-\pi}^{\pi}a_m cos^2(nt) dt = \pi a_n$$ |
| $$\int_{-\pi}^{\pi} f(t) sin(nt) dt = \int_{-\pi}^{\pi}b_m sin^2(nt) dt = \pi b_n$$ |
このことから、次の式で係数an、bnが計算できます。
| $$a_0 = \frac{1}{2\pi}\int_{-\pi}^{\pi} f(t) dt$$ $$a_n = \frac{1}{\pi}\int_{-\pi}^{\pi} f(t) cos(nt) dt$$ $$b_n = \frac{1}{\pi}\int_{-\pi}^{\pi} f(t) sin(nt) dt$$ |
以上のことを踏まえて矩形波のフーリエ係数は以下のようになります。
$$a_n = \int_{-\pi}^{\pi}f(t) cos(nt) dt = 0$$
$$b_n = \frac{1}{\pi}\int_{-\pi}^{\pi} f(t) sin(nt) dt = \frac{2}{\pi}\int_{0}^{\pi}\sin(nt) dt = \left \{ \begin{array}{1} \frac{1}{\pi n} & (nが奇数) \\ 0 & (nが偶数)\end{array}\right.$$
このことより矩形波のフーリエ級数展開は次のようになります。
$$f(t) = \frac{1}{\pi}\sum_{k=0}^{\infty} \frac{1}{2k + 1} sin(2k + 1)t$$
上記の式は無限級数になっていますが、実際の場合は、無限まで計算できませんので、途中で打ち切り、近似式を用います。これをフーリエ級数近似式といいます。以下が矩形波のフーリエ級数近似式です。
$$f(t) ≒ \frac{4}{\pi} \sum_{k=0}^{K} \frac{1}{2k +1}sin(2k + 1)t$$
Kの値が大きいほど近似は精度が高くなります。ここで、Kが0、1、3、7、15場合のフーリエ級数近似をグラフで示します。
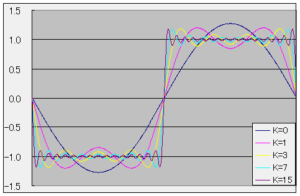
例2.鋸波
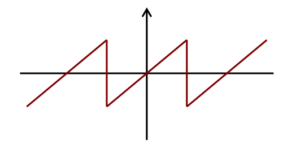
上のグラフのような周期関数を鋸波といいます。
$$f(t) = t, f(t + 2\pi) = f(t)$$
鋸波のフーリエ係数は、次のようになります。
$$a_n = \frac{1}{\pi}\int _{-\pi}^{\pi} t\, cos(nt) dt = 0$$
$$b_n = \frac{1}{\pi} \int_{-\pi}^{\pi}f(t) cos(nt) dt = \frac{1}{\pi} \left[-x\frac{cos(nt)}{n}\right]_{\pi}^{-\pi} + \frac{1}{\pi}\int_{-\pi}^{\pi} \frac{cos(nt)}{n} dt = (-1)^{n + 1}\frac{2}{\pi}$$
このことより鋸波のフーリエ級数近似式は以下のとおりです。
$$f(t) ≒ \sum_{n=0}^{N}(-1)^{n + 1}\frac{2}{\pi}\,sin(nt)$$
以下にNが1、3、7、15、31のフーリエ級数近似の1周期分を示します。
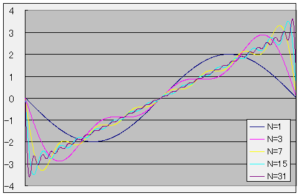
まとめ
まだ、デルタ関数を説明していませんのでインパルス波に関してのフーリエ級数は説明できませんが、インパルス波に関してもそれほど難しくありません。デルタ関数を説明した後にインパルス波についても言及すると思います。
今日の例題で、少しはフーリエ級数に関しての理解は深まったと思います。周期関数がフーリエ級数で表せるということがわかったと思います。ほかにも大学の講義で使う教科書にはフーリエ級数の例題がのっていると思いますので、そちらもよく読んで、フーリエ級数に関しての理解を深めてください。理系でフーリエ級数がわからないというのは致命傷ですので、頑張ってください。



他のサイトより非常に分かりやすく勉強させて貰っています。
ありがとうございます。
ただ分からないのは矩形波の変換で、nが奇数の時何故1/nπとなるのでしょうか。 何度計算しても4/nπとなるのですが。 私も積分苦手なので間違っているかも知れません。