$$\newcommand{\diff}{\mathrm{d}}$$
フーリエ級数を有限での近似でグラフで書くと不連続点の近似で凹凸が現われます。これは例えば矩形波を三角関数で表すことによる「無理」がそのようにして現われるのです。とは言え、無限でのフーリエ級数では不連続点での凹凸はなくなります。
この有限での近似で不連続点の近傍で現われる凹凸のことをギブス現象
といいます。それでは実際にギブス現象を見て行きましょう。
矩形波のフーリエ級数
ここで次のグラフのような矩形波を考えます。
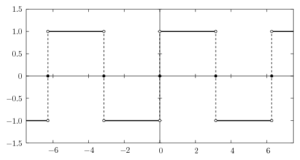
上のグラフは次の矩形波です。
$$\begin{align*}f(x) = \left\{\begin{array}{}1 && (2m\pi < x < (2m+1)\pi) \\ -1 && ((2m +1)\pi < x < (2m +2 )\pi) \\ 0 && ( 2m\pi = x ) \end{array}\right. && (1)\end{align*}$$
$$f(x)$$は周期$$2\pi$$の周期関数です。フーリエ級数は、以下のとおりです。
$$\begin{align*}f(x) \sim \frac{a_0}{2} + \sum_{n=1}^{\infty}\left(a_n\cos nx + b_n\sin nx\right) && (2)\end{align*}$$
フーリエ係数はそれぞれ$$\begin{align*}a_n = \frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos nx \diff x \\ && (3) \\ b_n = \frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\sin nx \diff x\end{align*}$$ここで、$$f(x)$$は奇関数ですので、$$a_n$$はすべて0になります。$$b_n$$は$$\begin{align*}b_n = \frac{2}{\pi}\int_{0}^{\pi}\sin nx \diff x = \frac{2}{n\pi}\left[-\cos nx\right]_{0}^{\pi} = \left\{\begin{array}{}\frac{4}{n\pi} && (nは奇数) \\ 0 && (nは偶数) \end{array}\right. && (4)\end{align*}$$となります。このことから$$f(x)$$のフーリエ級数表示は$$\begin{align*}f(x) = \frac{4}{\pi}\sum_{n=0}^{\infty}\frac{\sin(2n +1)x}{(2n +1 )} \\ = \frac{4}{\pi}\left(\sin x + \frac{1}{3}\sin 3x + \frac{1}{5}\sin 5x + \cdots\right) && (5)\end{align*}$$となります。
ギブス現象
(5)の右辺は$$\sin$$の無限和で表されていますが、実際に(5)を計算するときは有限和として計算します。そうしなければ、計算が終わりません。そこで(5)の部分和を考えます。
$$\begin{align*}f_N(x) = \frac{4}{\pi}\sum_{n=0}^{N}\frac{\sin(2n +1)x}{(2n + 1)} && (6)\end{align*}$$
ここで(6)のグラフをNの値を変えて書いてみます。
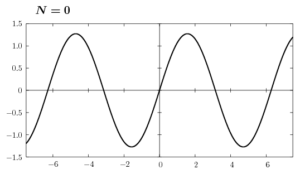
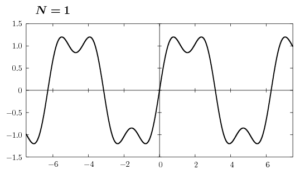
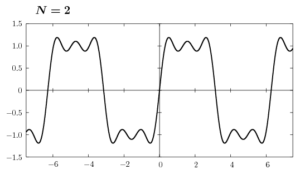
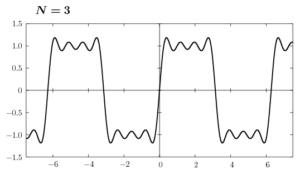
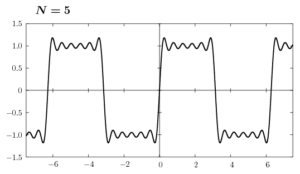
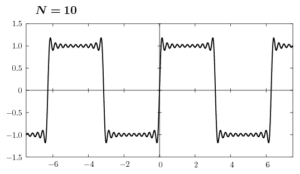
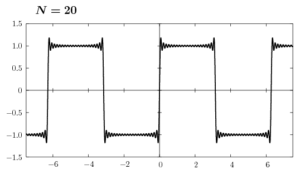
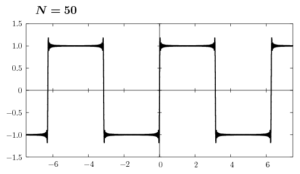
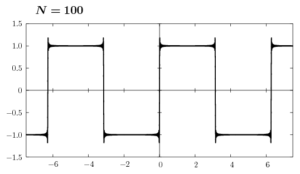
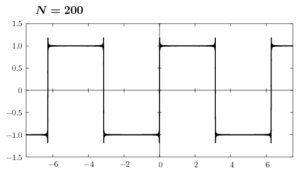
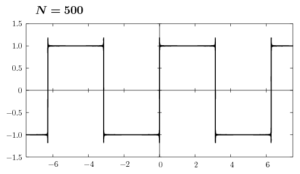
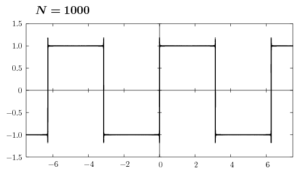
Nの値を大きくして行けば、矩形波に近付くのはわかると思います。しかし、不連続点の近傍ではギザギザした凹凸がNが有限の値である限り消えることはありません。これをギブス現象といいます。
まとめ
フーリエ級数は無限和を取ることであらゆる関数を三角関数で表せることができるというものです。しかし、実際の計算では無限和を計算することは不可能です。そこで、有限和で近似値を求めることでフーリエ級数の値の近似値を求め、その値でフーリエ級数の値としています。しかし、
有限和の値をグラフにすると不連続点の近傍でギザギザした凹凸が現われます。これをギブス現象
といいます。


