$$\newcommand{\diff}{\mathrm{d}}$$
ディラックのデルタ関数とは英国の物理学者、[keikou]ポール・ディラック[/keikou]によって考案された超関数と呼ばれるものです。これは、ある一点のみに非常に大きな値が存在し、そのほかは0という、例えば、大きさのない電荷や作用している時間が0の衝撃力を数式で表したいときに用いると大変便利なものが、ディラックのデルタ関数なのです。
単位階段関数(単位ステップ関数)とディラックのデルタ関数
単位階段関数は次のように表されます。
$$\begin{align*} u(x – \alpha) = \left\{\begin{array}{} 1 && (x \geq \alpha)\\ 0 && ( x < \alpha) \end{array}\right. && (1)\end{align*} $$
これを図で表すと下記のとおりです。

特に$$\alpha = 0$$のとき、これをヘビサイド関数ともいいます。そして、ディラックのデルタ関数は次のように定義されます。
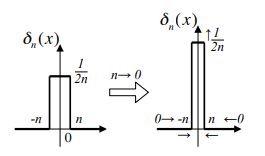
まず、上記の図のように、正の定数$$n$$に対して$$(-n \leq x \leq n)$$のときのみ$$\frac{1}{2n}$$の値をとり、それ以外は$$0$$をとる方形関数を考えます。
$$\begin{align*}\delta_n(x) = \left\{\begin{array}{} \frac{1}{2n} && (-n \leq x \leq n) \\ 0 && (x < n, n <x)\end{array}\right. && (2)\end{align*}$$
ここで、この関数の面積(長方形の面積)は$$n$$がどんなに変化しようが、$$2n\times\frac{1}{2n} = 1$$となって一定です。

そして、$$n \rightarrow 0$$の極限をとって、上記の図のように$$x = 0$$のときのみ$$\infty$$となり、それ以外のとき$$0$$の値をとります。これがディラックのデルタ関数です。
単位階段関数とディラックのデルタ関数の関係
これで単位階段関数とディラックのデルタ関数の関係が分かると思います。つまり、(1)~(8)から単位階段関数とディラックのデルタ関数の関係は次のとおりです。
(9),(10)はのちのフーリエ変換やラプラス変換など、その用途は多岐にわたりますので、しっかりと覚えてください。
まとめ
ここではディラックのデルタ関数の性質とその積分、そして、単位階段関数(単位ステップ関数)とディラックのデルタ関数との関係を見てきました。正確にいえばディラックのデルタ関数は関数ではなく、超関数というものなのです。しかし、ディラックのデルタ関数は色々な所で利用されますので、その性質をよく覚えてください。

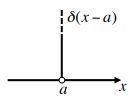 $$\begin{align*}\delta(x – \alpha) = \left\{\begin{array}{}\infty && (x = \alpha) \\ 0 && (x \neq \alpha)\end{array}\right. && (6)\end{align*}$$
$$\begin{align*}\delta(x – \alpha) = \left\{\begin{array}{}\infty && (x = \alpha) \\ 0 && (x \neq \alpha)\end{array}\right. && (6)\end{align*}$$


≪…ディラックのデルタ関数は関数ではなく、超関数…≫は、直交座標を与えるモノと観える。
『自然比矩形』の[e]を[n]とし,[n]を[1]にすると、[1 0 ∞]の数学思考作用により、
[縦軸]と[横軸]が顕現すると観る。
この原型は、絵本「もろはのつるぎ」(有田川町ウエブライブラリー)