$$\newcommand{\diff}{\mathrm{d}}$$
私たちの身の回りを見れば、そこにはさまざまな波が存在しているのが分かります。例えば光の波の重ね合わせによる光のスペクトル、地震、気候現象、断層配列などなど上げれば枚挙に暇がありません。波といえばフーリエ変換が思い出されるはずです。ここではスペクトルとフーリエ変換の関係を取り上げます。
時系列データをスペクトル解析する
時系列データをスペクトル解析(周波数解析、フーリエ解析などともいう)するための原理を説明して行きます。時系列データとスペクトルはフーリエ変換とフーリエ逆変換がその関係を取り結んでいます。
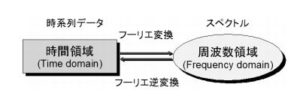
上図が示すとおりなのです。ここで説明することは上図のことなのです。
フーリエ変換とスペクトル
フーリエ変換は覚えていますか？複素フーリエ級数を拡張したものがフーリエ変換とフーリエ逆変換でしたね。
関数$$f(x)$$に関してフーリエ変換とフーリエ逆変換は次のとおりです。 フーリエ変換 $$\begin{align*}f(x) = \int_{-\infty}^{\infty}F(\omega)\mathrm{e}^{i\omega x}\diff\omega && (1)\end{align*}$$ フーリエ逆変換 $$\begin{align*}F(\omega) = \frac{1}{2\pi}\int_{-\infty}^{\infty}f(x)\mathrm{e}^{-i\omega x}\diff x && (2)\end{align*}$$
ここで問題になるのは時間です。そこで$$x \rightarrow 時間t$$に、そして$$\omega$$を角周波数(振動数$$f$$のとき角周波数は$$\omega = 2\pi f$$)とでフーリエ変換とフーリエ逆変換を書き換えると、
$$\begin{align*}f(t) = \int_{-\infty}^{\infty}F(\omega)\mathrm{e}^{i\omega t}\diff\omega && (3)\end{align*}$$
$$\begin{align*}F(\omega)= \frac{1}{2\pi}\int_{-\infty}^{\infty}f(t)\mathrm{e}^{-i\omega t}\diff t && (4)\end{align*}$$となります。そして、スペクトルは不規則変動という様々な波の重ね合わせで、つまり、フーリエ変換で表されるのです。
$$\begin{align*}f(t) = \int_{-\infty}^{\infty}F(f)\mathrm{e}^{i2\pi ft}\diff f && (5)\end{align*}$$
(5)の$$f$$は当然周波数のことです。ここで、フーリエ成分$$F(f)$$は周波数$$f$$の波$$\mathrm{e}^{i2\pi ft}$$の振幅を表し、$$|F(f)|^2$$はそのエネルギーを表します。
エネルギースペクトル密度
エネルギースペクトル密度とは信号のエネルギーが周波数に対してどのように分布するかを表したもので、つまり、周波数$$f$$に対するエネルギー$$|F(f)|^2$$の分布のことです。
$$\begin{align*}\Phi(f) = |F(f)|^2 && (6)\end{align*}$$
パワースペクトル密度
有限区間での周期関数や例えば周期を$$T$$とした場合、$$(-\frac{T}{2}, \frac{T}{2})$$以外では変動しない場合、エネルギーが有限値の$$|F(f)|^2$$となりますが、これが区間$$T$$が無限のとき、エネルギーも無限大になってしまいます。そこで、単位時間あたりの平均エネルギーを考えたものがパワースペクトル密度です。
$$\begin{align*}P(f) = \lim_{T \rightarrow\infty}\frac{|F(f)|^2}{T} = \lim_{t\rightarrow\infty}\frac{F(f)・F^*(f)}{T} && (7)\end{align*}$$
ここで$$F^*(f)$$は$$F(f)$$の共役複素数です。また、単位時間あたりの平均エネルギー(単位時間あたりの平均エネルギーをすべての周波数で足したもの)は、
$$\begin{align*}\dot{x^2} = \lim_{T\rightarrow\infty}\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}x^2(t)\diff t = \int_{-\infty}^{\infty}P(f)\diff f && (8)\end{align*}$$
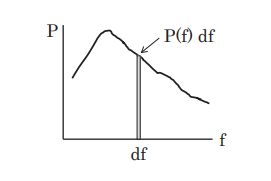
となります。これは周波数$$f$$と$$f + \diff f$$の間に含まれる成分波の変動エネルギー$$\dot{x^2}$$への寄与率を表していて、スペクトル$$P(f)\diff f$$ともみなせます。
(7)もしくは(8)で表される関係式が「原義的なスペクトル$$P(f)$$の定義｣です。
まとめ
今回は周りにある波、例えばスペクトルがフーリエ変換で表されることを見てきました。[keikou]時間と角周波数とでフーリエ変換とフーリエ逆変換を表せば、自然に満ちあふれている不規則変動がすべてフーリエ変換とフーリエ逆変換で表されるのです[/keikou]。光のスペクトル、地震波、気候現象など、あらゆるものがフーリエ変換とフーリエ逆変換とで表せるのです。つまり、フーリエ変換とフーリエ逆変換は大変重要なものなのです。
