$$\newcommand{\diff}{\mathrm{d}}$$
フーリエ級数、リーマン・ルベーグの補助定理と学んできましたが、今回はフーリエの収束定理の証明をしていきます。ここで、「ディリクレ核」というものが登場しますが、そちらも説明したいと思います。
フーリエの収束定理は、その名から予想されるとおり極限値を求めるもので、その証明は多少複雑ですが、なんとかついてきてください。
証明したいこと
まず、
フーリエ級数を有限数Nまでの和をとったものをSN(x)を考えます
。それは以下のとおりです。
$$S_N(x) = \frac{1}{2}a_0 + \sum_{N=1}^{N}(a_n\cos\,nx + b_n\sin\,nx)\tag{1}$$
フーリエ級数f(x)は次のとおりです。
$$f(x) = \frac{1}{2}a_0 + \sum_{n=1}^{\infty}(a_n \cos\,nx + b_n\sin\,nx)\tag{2}$$
それで証明したいことは次のものです。
(3)に(1)を代入すると
$$\lim_{N \to \infty}\left[\left\{\frac{1}{2}a_0 + \sum_{N=1}^{N}a_n\cos\,nx + b_n\sin\,nx)\right\} -f(x)\right] = 0\tag{4}$$
$$a_0、a_n、b_nはフーリエ係数で次のとおりでしたね。$$
(5)のフーリエ係数を(4)に代入します。ただし、関数そのものの独立変数はx、フーリエ係数部分の積分変数は「y」にします。
$$\lim_{N \to \infty}\left(\frac{1}{2}\left\{\frac{1}{\pi}\int_{-\pi}^{\pi}f(y)\diff y \right\}+ \sum_{n=1}^{N}\left[\left\{\frac{1}{\pi}\int_{-\pi}^{\pi}f(y)\cos\,ny\diff y\right\}\cos\,nx \\ + \left\{\frac{1}{\pi}\int_{-\pi}^{\pi}f(y)\sin\,ny\diff y\right\}\sin\,nx\right] – f(x)\right) = 0\tag{6}$$
ディリクレ核の導出
上式(6)はとてもごちゃごちゃしていますね。これを整理したいと思います。(6)で$$S_N(x)$$の部分を整理します。
$$\begin{align*}S_N(x)= \lim_{N \to \infty}\frac{1}{2}\left\{\frac{1}{\pi}\int_{-\pi}^{\pi}f(y)\diff y \right\}+ \sum_{n=1}^{N}\left[\left\{\frac{1}{\pi}\int_{-\pi}^{\pi}f(y)\cos\,ny\diff y\right\}\cos\,nx \\ + \left\{\frac{1}{\pi}\int_{-\pi}^{\pi}f(y)\sin\,ny\diff y\right\}\sin\,nx\right] \\ = \frac{1}{\pi}\int_{-pi}^{\pi}f(y)\times\left\{\frac{1}{2} + \sum_{n=1}^{N}\left\{\cos\,ny\cos\,nx + \sin\,ny\sin\,nx\right\}\right\}\diff y\end{align*} \tag{7}$$
ここで、$$\sum_{n=1}^{N}の\left\{\right\}内に注目すると$$
の形をしていますね。それにより、
ここで、z = y – xとすれば、yはzで置き換えられます。
積分変数をyからzに変えますので、積分区間も修正されます。
よって$$S_N(x)$$は次のようになります。
$$\begin{align*}S_N(x) = \frac{1}{\pi}\int_{-\pi}^{\pi}f(y)\times\left\{\frac{1}{2} + \sum_{n=1}^{N}\cos\left\{n(y – x)\right\}\right\}\\ = \frac{1}{\pi}\int_{-\pi – x}^{\pi – x}f(x + z)\times\left\{\frac{1}{2} + \sum_{n=1}^{N}\cos \,nz\right\}\diff z\end{align*}\tag{9}$$
ここで、積分区間の$$-\pi -x と\pi -x$$がなんとなくですが、すっきりしませんね。
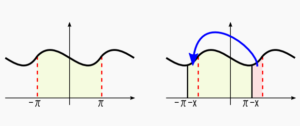
上図を見てください。周期関数の場合、積分区間をずらしても積分の値は変わらないということがわかります。よって(9)は次のようになります。
$$\begin{align*}S_N(x) = \frac{1}{\pi}\int_{-\pi-x}^{\pi -x}f(x + z)\times\left\{\frac{1}{2} + \sum_{n=1}^{N}\cos\,nz \right\}\diff z \\ = \frac{1}{\pi}\int_{-\pi}^{\pi}f(x + z)\times\left\{\frac{1}{2} + \sum_{n=1}^{N}\cos\,nz\right\}\diff z\end{align*}\tag{10}$$
この(10)の$$\left\{\right\}内、つまり、\frac{1}{2} + \sum_{n=1}^{N}\cos\,nz$$はディリクレ核と呼ばれるものです。ディリクレとはフーリエの弟子だった人の名です。(10)は特別にD(x)という記号で表します。そして、D(x)は次のような式を導きます。
$$D_N(x) = \frac{1}{2} + \sum_{n=1}^{N}\cos\,nz \tag{11}$$
(11)の両辺に$$2\sin\left(\frac{1}{2}x\right)$$をかけます。
$$\begin{align*}2\sin\left(\frac{1}{2}x\right)\times D_N(x) & = 2\sin\left(\frac{1}{2}x\right)\times\left\{\frac{1}{2} + \sum_{n=1}^{N}\cos\,nz\right\} \\ & = 2\sin\left(\frac{1}{2}x\right)\times\frac{1}{2} + 2\sin\left(\frac{1}{2}x\right)\times\cos \,x + 2\sin\left(\frac{1}{2}x\right)\times\cos\,2x \\ & + \cdots + 2\sin\left(\frac{1}{2}x\right)\times\cos\,Nx \\ & = \sin\left(\frac{1}{2}x\right) + \left\{\sin\left(\frac{1}{2} – 1\right)x + \sin\left(\frac{1}{2} +1\right)x\right\} + \left\{\sin\left(\frac{1}{2} – 2\right) + \sin\left(\frac{1}{2} + 2\right)x\right\} \\ & + \cdots + \left\{\sin\left(\frac{1}{2} – N\right) + \sin\left(\frac{1}{2} + N\right)x\right\} \\ & = 0 + 0 + \cdots + \sin\left(\frac{1}{2} + N\right)x \\ & = \sin\left(\frac{1}{2} + N\right)x\end{align*}$$
というわけで次式が導かれました。
$$2\sin\left(\frac{1}{2}x\right)\times D_N(x) = \sin\left(\frac{1}{2} + N\right)x$$
上式からディリクレ核は次のようになります。
以上のことから(6)は次のようになります。
$$\lim_{N \to \infty}\left[\frac{1}{\pi}\int_{-\pi}^{\pi}f(x + z)\times\left\{\frac{1}{2} + \sum_{n=1}^{N}\cos\,nz\right\}\diff z – f(x)\right] = 0\tag{13}$$
(13)にディリクレ核を代入しますと、
$$\lim_{N \to \infty}\left[\frac{1}{\pi}\int_{-\pi}^{\pi}f(x + z)\times\frac{\sin\left(\frac{1}{2} +N\right)}{2\sin\left(\frac{1}{2}z\right)} – f(x)\right] = 0$$
上式を少し変形します。
$$\lim_{N \to \infty}\left[\frac{1}{\pi}\int_{-\pi}^{\pi}\frac{\left\{f(x + z) – f(x)\right\}}{2\sin\left(\frac{1}{2}z\right)}\times\sin\left(\frac{1}{2} + N\right)z\diff z\right] = 0\tag{14} $$
(14)をよく見るとリーマン・ルベーグの補助定理に似ていると思いませんか。リーマン・ルベーグの補助定理は次のとおりです。
しかし、リーマン・ルベーグの補助定理を満たすには(15)のf(x)が発散しないことです。それではもう一度(14)を見てみますと、f(x)に当たる部分は、
$$\frac{\left\{f(x + z) – f(x)\right\}}{2\sin\left(\frac{1}{2}z\right)}\tag{16}$$
ですね。上式の分母は0になる場合があります。そこで、上式の極限値を見てみましょう。
$$\begin{align*}\lim_{z \to 0}\frac{f(x + z) – f(x)}{2\sin\left(\frac{1}{2}z\right)} & = \lim_{z \to 0}\left\{\frac{f(x + z) – f(x)}{z}\times\frac{\frac{1}{2}z}{\sin\left(\frac{1}{2}z\right)}\right\}\end{align*}\tag{17}$$
(16)の右式の前段はf(z)の微分です。問題は後段のsinです。
$$\lim_{z \to 0}\frac{\frac{1}{2}z}{\sin\left(\frac{1}{2}z\right)}\tag{18}$$
(18)は1に収束することはよく知られています。つまり、(16)は発散しないのです。これでようやくフーリエの収束定理の証明の終点にきました。
まとめ
今回はフーリエの収束定理の証明をしてみましたが、たいへん骨が折れました。わかったでしょうか。いっていることはとても簡単なのですが、それを証明するにはディリクレ核やリーマン・ルベーグの補助定理など、これまで学んだことの総動員です。それでも何とか証明することができました。
このような基礎的なことを証明するのが一番難しいものです。今回のフーリエの収束定理はフーリエ級数の土台を作っているものです。できうる限り解りやすく証明してきたのですが、どうでしょうか。わからない点があれば、もっと深く自分で掘り下げてみてください。


