極座標って必要なのかな・・・なんで変換が必要なんだろう？？？
極座標はいいぞぉ！場合によってはとんでもなく楽できるからな・・・
ということで、今回のテーマは二次元の直交座標と極座標についてです。なんとなく定義については知っている人もいるかもしれませんが、ここでは、直交座標と極座標の変換方法を紹介します。
また、「コレってなんの使い道が？」と思われる方もいると思うので、その利便性もご紹介します。
直交座標とは
直交座標は別名、デカルト座標とも呼ばれます。
直交座標は\(P(x,y)\) で点の位置を表す方法 である
この表し方は、中学校の頃からみなさん親しみがあると思います。名前の由来は言わずもがな、\(x\) 座標と \(y\) 座標が直交していることに由来しています。
この直交座標系は物理学では、物体の直線運動や放物線運動を表すときに使われます。また、中学校で習う理科でも、グラフなんかを何度も使ってきているので、使い道のイメージはすぐ湧くと思います。問題は高校数学で初めて習う、極座標のほうですよね。
極座標とは
ひとまず定義から見ていきましょう。
極座標は \(P(r,θ)\) で点の位置を表す方法 である
\(r\) ：極\(O\)から点\(P\)までの距離\(θ\)：点\(P\)を見上げる角度（偏角）
この極座標系は物理学では、物体の円運動を表すときに使われます。
直交座標系と極座標系の変換について
さて、ひき続きそれぞれの方向からの変換の公式をみてみましょう。
極座標 \((r,θ)\) から直交座標 \((x,y)\) への変換
\(x=rcosθ\) ，\(y=rsinθ\)
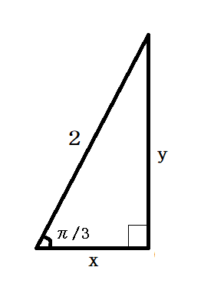
例
\((r,θ)=(2,\frac{\pi}{3})\) のとき、それぞれ代入すると \(x=1,y=\)\(\sqrt{3}\)
となるため、\((x,y)=(1,3)\) と表すことができる。
メリット
- 点と二つの実数の組 \((x,y)\) が１対１対応である
- 見た目に表しやすい
まあこっちのほうが使い慣れてるんだから、今更メリットも何もないよな。
直交座標 \((x,y)\) から極座標 \((r,θ)\) への変換
\(r=\sqrt{x^2+y^2}\) ，\(cosθ=\frac{x}{\sqrt{x^2+y^2}}\) ，\(sinθ=\frac{y}{\sqrt{x^2+y^2}}\)
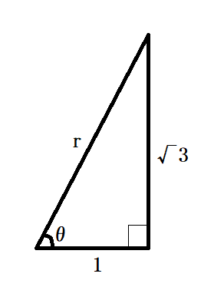
例
\((x,y)=(1,\sqrt{3})\) とき、それぞれ代入すると \(r=2\) , \(cosθ= \frac{1}{2}\) , \(sinθ\) = \(\frac{\sqrt{3}}{2}\)
となるため、\((r,θ)=(2,\frac{\pi}{3})\) と表すことができる。
メリット
- 物理学などで使いやすい（距離や角度で表すから）
- 円などの曲線は表しやすくなったり計算が楽になったりする
え！こんなに苦労したのに。たったそれだけですか・・・
まあ実際やってみないとよさがわからないよな～。
それでは、具体的な計算を見ていきたいと思います。
極座標変換を使った計算
極座標変換を使うのは、球面や球体積を求める場合が多いです。
直交座標系では、微小面積 \(dS=dxdy\) で表されていますが、一方で極座標系では、半径\(r\) の方向の微小な長さの幅 \(dr\) , 偏角 \(θ\) 方向の微小な長さは \(rdθ\) で表されるため、\(dS=rdrdθ\) で表されます。
よって、面積を
\(\int dS = \iint dxdy = \iint rdrdθ\)
と表すことができるのです。
そして、一番問題となるのが「なぜ変換する必要があるのか？」ですよね。
面積や体積はいつも都合よく直線ばかりじゃないからな
そうなんですよね。そんなに都合よく、毎回面積・体積が直線ばかりなわけないですよね！
数学の問題では、結構長方形の面積やら三角形の面積やらを求めて来ましたが、よくよく考えると都合良すぎませんか？確実に数学の計算用の面積ですよね。実生活においては直線しかないなんてことはあり得ないですから。
では、どんなときに使えそうか例をみてみましょう。
円の内部及び周 \(x^2+y^2 \leq 1\)を領域 \(D\) とするとき
二重積分 \(\iint_D xydxdy\) を計算せよ[/topic]
これは、直交座標では
\(\int_ {-1}^1\)\((\int_{-\sqrt{1-x^2}}^\sqrt{1-x^2}\)\( f_{(x,y)}dy)dx\)
と表すことができます。
範囲にルートがある・・・計算面倒くさそー・・・。
そうなんですね。範囲に \(\sqrt{ }\) が含まれているとのちのち式を整理したりするのも結構面倒なんですよね。
ここで、極座標への変換が使えます。この式を極座標に変換すると、
\(\int_0^1 \frac{r^2}{2}dr \int_0^2\pi sin2θdθ\)
\(= r^2 \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} cos^2 θdθ\)
\(=2r^2 \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac{1+cos2θ}{2} dθ\)
\(=2r^2[θ＋\frac{sinθ}{2}]_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\)
\(\pi r^2\)
となり、かなり簡単に計算できるようになるんです。\(\sqrt{ }\) もなくなりましたね。
このように、円の面積・体積などを求めたいようなときには極座標を使ったほうが計算が楽になるんです。
確かにこれでだいぶ楽に計算できるぞ！これだったら俺にもできそうだ！
なんかやる気出てきた！！！
数学って難しく見えるけど、やってくうちに、より楽な方法が身につくんだ。
勉強するほど、内容が難しくなって嫌だと思う人もいるだろうが、
むしろ今までやってきたことがさらに楽にできるようになるんだよ。
ゲームで言うと、レベルを上げたり新しい武器を手に入れる感じですね！
そうそう。レベル５の敵と戦うにはレベル１では辛いが、レベル10だと楽勝だろ！
レベル上げは時間もかかるし、面倒だと思うかもしれないが、必要だよな。
先生・・・俺、なんか数学の勉強がつらくなくなってきたかも！
というわけで、なんとなく実用性を感じることが出来たでしょうか。もちろん極座標に限らず、数学の勉強の必要性も感じてもらえると嬉しいです。
動画解説で、基礎から復習してくれています。是非参考にしてください。
めっちゃええ声なんです、この人
