さて、区分的といってど のような数学的なものを思い浮かべるでしょうか。何かの区分？であることは多分、間違いないと思うのですが、それが数学的にはどうなのか、と問われれば返答に困ってしまうのではないでしょう。
ここでは区分的とは何かを数学的に定義して、そして、なおさらわからない、区分的滑らか区分的連続とは？についても説明してゆきます。ただし、この区分的滑らか区分的連続とは？はフーリエ解析でとても大切なのでしっかりと理解してください。
区分的とは？
たとえば区間[a, b]を考えます。区間[a, b]上の関数f(x)に関してa = x0 < x1 < x2 ……< xn = bのように区間[xi-1, xi]に分けた各区間で成立する性質のことを区分的といいます。これだけ聞いてもなんのことかさっぱりわからないという人もいると思います。
かみ砕いていうと区間[a, b]をとても細かく区切って、そのときに関数f(x)が成立する場合のことを区分的というのです。どこか微分と関係が深そうだということは、ここから推察できると思います。
区分的滑らかとは？
さて、本題に入ります。区分的滑らかとはどのような状態のことをいうのでしょうか。
定義１
関数f(t)が次の①と②と満たすとき、区間[a, b]で区分的に滑らかといいます。
①[a, b]で有限個のt1,t2,……,tnを除いたところでf(t)は微分ができて、区間[a, b]の範囲で導関数f‘(t)は連続であるときです。
②不連続点tk(1≦k≦n)でf(t))およびf‘(t)の左側極限と右側極限が存在して、それが有限なときです。
a < tk < bのときは $$f(t_k – 0) =\lim_{h \to 0 \\ h > 0} f(t_k – h), f(t_k + 0) = \lim_{h \to 0 \\ h > 0} f(t_k + h)$$ $$f'(t_k – 0) = \lim_{h \to 0 \\ h > 0} f'(t_k – h), f'(t_k + 0) = \lim_{h \to 0 \\ h > 0} f'(t_k + h)$$ が存在して有限です。 $$t_k = aのときは右の極限f(t_k +0)、f'(t_k + 0)は有限で存在します。$$ $$t_k = bのときは左の極限f(t_k – 0)、f'(t_k – 0)は有限で存在します。$$
定義２
f(t)が周期2pの周期関数とします。この関数が[-p, p]上で区分的に滑らかなとき、f(t)を単に区分的に滑らかといいます。
たとえば、次の図は区分的滑らかなのです。
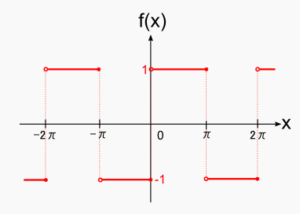
$$関数にすればまず[-\pi, \pi]では$$
$$f(x) =\left\{\begin{array}{1} -1 & (-\pi ≦ 0) \\ 1 & (0 ≦ \pi)\end{array}\right.$$
$$この図の関数の一般の形は周期2\piですので$$
$$f(x) =\left\{\begin{array}{1} -1 & (2n – 1)\pi ≦ x ≦ 2n\pi \\ 1 & 2n\pi ≦ x ≦ (2n + 1)\pi\end{array}\right. ここでnは整数です。$$
この例はとてもわかりやすいと思いますがどうでしょうか。
区分的連続とは？
まず、{t: a ≦ t ≦ b}を[a, b]とします。
関数f(t)が次の条件①と②を満たすとき、区間[a, b]で区分的に連続であるといいます。
①区間[a, b]に属する有限個の点t1,t2,……,tnを除いたところでf(t)は連続であるとき。
②各不連続点tk(1 ≦ k ≦ n)でf(t)の左側極限と右側極限が存在し、それが有限の値であるとき。
a < tk < bのとき $$f(t_k – 0) = \lim_{ h \to 0 \\ h > 0} f(t_k – h), f(t_k + 0) = \lim_{h \to 0 \\ h > 0} f(t_k + h)$$ が存在し、それは有限の値です。tk = aのときは右の極限f(tk + 0)が存在し、それは有限の値です。tk = bの時は左の極限f(tk – 0)が存在し、それもまた有限の値です。
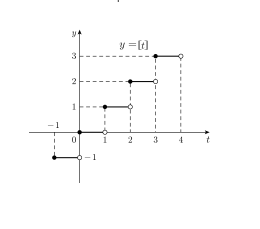
上の図は天井関数と呼ばれるものです。つまり、tを超えない最大整数がというのが天井関数で次のように表します。
$$f(t) = \lceil t \rceil$$
この場合、不連続点はt = k(kは整数)のときのみです。よってf(t)は任意の有限区間で区分的連続です。t = k(整数)のときはf(k – 0) = k – 1、f(k + 0) = kです。
まとめ
区分的滑らかと区分的連続とは、一階導関数が関係するかどうかの違いです。区分的滑らかとはある区間に有限個の不連続な点が存在してもその他が連続で、また、一階導関数で連続な場合、区分的滑らかといい、一階導関数までは考えない場合を区分的連続といいます。
これは後々フーリエ解析でとても大切なものとして登場しますので、区分的滑らか区分的連続とは？の？マークを取り除いてください。ここでは簡単な例題で区分的滑らかと区分的連続を示していますので、理解できたと思います。
区分的滑らか区分的連続の定義はそれだけ読んでも曖昧模糊としていると思いますが、例題を見れば区分的滑らかと区分的連続がなんなのかわかったはずです。ここで、フーリエ解析でつまづかないようにしっかりと理解しておきましょう。
