接平面の方程式とは？【公式と証明方法＋具体例】をす・べ・て紹介！

なんだか難しそうな内容だなあ・・・やりたくない。

今回のテーマは「接平面」です。

ここでは、接平面の方程式を主なキーワードとしてやっていきます。

証明方法と計算例を示してあるので、学習で必要な人は参考になると思いますよ。

さあ、嫌がらずに、やってみよう！１回やってみればできる内容だぞ！

接平面とは

ある２変数関数 \(z=f(x,y)\) が表している曲面に接する平面を接平面といいます。

つまり、曲面上の一点で、この曲面に引いた接線をすべて含む平面が接平面であるといえます。

下図の面が接平面です。

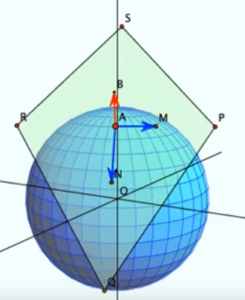
※下にリンクが貼っている動画から取り出した画像です。

接平面の方程式（接平面の定義）

接平面の方程式の公式は以下の通りになります。

【証明】

\(z=f(x,y)\) の接点が \((x_0,y_0,f(x_0,y_0))\) であるとき、この接平面は \(x\) 軸方向の接線 \(L\) と\(y\) 軸方向の接線\(l\) を含む。それぞれの方程式は、

\(L:y=y_0 ,z=f_x(x_0,y_0)(x-x_0)+f(x_0,y_0)\)

\(l:x=x_0,z=f_y(x_0,y_0)(y-y_0)+f(x_0,y_0)\)

である。ここで、接平面の方程式を \(z=mx+ny+k\) とおくと、

(ⅰ) \(x\) 軸方向の傾き：\(m=f_x(x_0,y_0)\)

(ⅱ) \(y\) 軸方向の傾き：\(n=f_y(x_0,y_0)\)

であり、\((x,y)=(x_0,y_0)\) のとき \(z=f(x_0,y_0) \)より

\(f(x_0,y_0)=mx_0 +ny_0 +k\) であるから

（ⅲ）\(z\) 切片 \(k=f(x_0,y_0)-mx_0 -ny_0\)

となる。ゆえに(ⅰ)(ⅱ)(ⅲ)より、接平面の方程式は

\(f_x(x_0,y_0)(x-x_0)+f_y(x_0,y_0)(y-y_0)+f(x_0,y_0)\)

なるほど、この前習った偏微分が出てくるんだ！

例題

\(f(x,y)=x^2+3xy\) のとき \((x,y)=(1,-2)\) における接平面の方程式を求めよ。

\(f_x(x,y)=2x+3y\) , \(f_y(x,y)=3x\) より、

\(f_x(1,-2)=-4\) , \(f_y(1,-2)=3\) , \(f(1,-2)=-5\)

よって接平面の方程式は、\(z=-4(x-1)+3(y+2)-5\)

ゆえに \(z=-4x+3y+5\)

というわけで、定義をみると、変数や定数の文字がゴチャゴチャしていて難しそうに見えるが、実際の計算はかなり簡単なものだっただろう！

なんか思ったよりも、全然簡単だった！これだったらオレでもできそう！

接平面の図は書くのが難しいので、イメージはこちらを参考にしてください