転置行列とは？定義と４つの性質を証明してみた

さて、今回は行列のなかでも特徴的な転置行列についてです。

転置行列ってなんだっけなぁ・・・

転置行列は行列の中でも重要な役割を果たす行列だ！

しっかり押さえておこう！

今回は定義と重要な４つの性質についてまとめました。

それでは、確認してみましょう！

1 転置行列の定義
2 転置行列の４つの性質

転置行列の定義

\(ij\) 成分が \(a_{ij}\) であるような行列を \(A\) とする。このとき \(a_{ji}\) を \(ij\) 成分とするような行列を \(A\) の転置行列と言い、\(A^t\) などと表します。

なるほど！縦と横が逆になったイメージか！！！

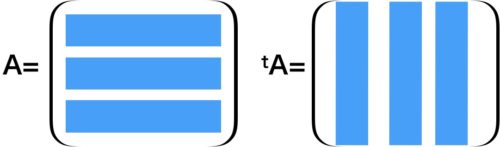
この画像を頭に入れておくと、覚えやすいぞ！

\(A=\begin{pmatrix}1&2\\3&4 \end{pmatrix}\)のとき、その転置行列は \(A^t=\begin{pmatrix}1&3\\2&4 \end{pmatrix}\)と表します。

転置行列の４つの性質

さて、転置行列には４つの大切な性質がありますので、押さえておきましょう！

ポイント

行列 \(A\) に対して、転置行列 \(A^t\) では以下の性質が成り立つ。

　　①　\((A^t)^t=A\)

　　②　\((A+B)^t=A^t+B^t\)

　　③　\((kA)^t=kA^t\)

　　④　\((AB)^t=B^tA^t\)

それぞれ具体例で性質を確認してみましょう。

\(A=\begin{pmatrix}1&2\\3&4 \end{pmatrix}\) , \(B=\begin{pmatrix}5&6\\7&8 \end{pmatrix}\)　

として、みなさんも是非答えを見る前に一度自分で計算をしてみてくださいね！

うーむ・・・計算頑張ればいけそうだ・・・

このくらいの計算はできて当たり前だろう！

◆解答◆

①　\((A^t)^t\)\(={\begin{pmatrix}1&3\\2&4\end{pmatrix}}^t\)\(=\begin{pmatrix}1&2\\3&4 \end{pmatrix}\)\(=A\)

②　\((A+B)^t\)\(\{\begin{pmatrix}1+5&2+6\\3+7&4+8 \end{pmatrix}\}^t\)\(=\begin{pmatrix}6&8\\10&12\end{pmatrix}\)\(=\begin{pmatrix}1&3\\2&4 \end{pmatrix}+\begin{pmatrix}5&7\\6&8 \end{pmatrix}\)\(=A^t+B^t\)

③　\((kA)^t\)\(={\begin{pmatrix}k&2k\\3k&4k\end{pmatrix}}^t\)\(=\begin{pmatrix}k&3k\\2k&4k\end{pmatrix}\)\(=kA^t\)

④　 \((AB)^t\)\(={\begin{pmatrix}19&24\\43&50\end{pmatrix}}^t=\begin{pmatrix}19&43\\24&50\end{pmatrix}=\begin{pmatrix}5&7\\6&8\end{pmatrix}\begin{pmatrix}1&3\\2&4\end{pmatrix}=B^t A^t\)