フーリエ級数と聞いただけで、数式に対して拒否反応が出るという人も少なくないのではないでしょうか。
しかし、世界を見ると周期的な動きを見せるものが非常に多いことに気づくはずです。
簡単なところでは地球の公転、つまり、一年365日ということは周期的です。
一日が24時間ということも同様です。
これはあくまで一例ですが、自然現象は周期的な様相を呈することが非常に多いのです。
フーリエはそんな中で熱伝導をなんとか三角関数で表せないかと悪戦苦闘し、フーリエ級数展開を見出しました。
フーリエはその時にこの世の森羅万象はすべて三角関数で表せると豪語し、世の反発を招きましたが、その後、研究が進み、フーリエが見出したものは多くの物理現象や株式の世界でも適応できることが現在知られています。
そんなフーリエが見出したフーリエ級数展開をここでは取り上げます。
フーリエ級数展開にいきなり出てくる難しい公式
フーリエ級数展開で「あちゃあ!」とたじろがせるのが最初に出てくるフーリエ級数展開の見るからに難しい公式です。
次の式を見てなんのことかわかるという人は物理学をかじったことがある人か、数学をかじったことがある人です。
まず、実数値関数のフーリエ級数は以下の通りです。
さあ、これは困りましたね。一体上記のことは何を意味しているのでしょうか。
次の図を見てください。
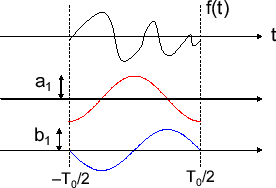
これは余弦係数が1周期、正弦係数も1周期のときに上記で定義したフーリエ級数展開が$$f(t)$$のようになることを図で表したものです。
つまり、
$$cos(nt)とsin(nt)$$
を足してゆくのですが、それは周期的な動きを示していて、それを重ね合わせたものがフーリエ級数展開なのです。
上記のフーリエ級数展開でほとんどの周期的なものが表されることは理解できるでしょうか。
$$a_nもb_nも$$
様々に数値を変え、$$cos(nx)もsin(nx)も$$
様々な波の波形を表すのです。
それを重ね合わせれば、大変複雑な周期を持つ現象をフーリエ級数展開で表せることがなんとなくでもわかるはずです。
フーリエ級数展開は決して難しいことを述べているのではなく、ごく普通のありふれた自然現象や株式の動きなど、波形で表せるものはなんでもフーリエ級数展開で置き換えることが可能なのです。
オイラーの公式を使った複素数値関数のフーリエ級数展開がある
フーリエ級数展開はなにも実数に限らずに複素数でも成り立つのです。
それはここでは深く立ち入りらず、 またの機会に説明しますが、次へのように定義できます。
$$c_n = \frac{1}{2\pi}\int_{-\pi}^{\pi} f(t) e^{-int} dt,(n = 1, 2, 3,……)$$
$$ここでfをフーリエ係数といいます。$$
複素数に関したてはまたの機会に説明しますが、フーリエ級数展開を用いれば、たいていの自然現象が説明できてしまうのです。
フーリエは熱伝導をなんとか数式で表すことに血肉を注ぎましたが、その研究が現在実を結び、あらゆる分野に応用されているのです。
動画の紹介
う~ん、この動画ではまだ、フーリエ級数展開に関してピンとこないという人が多いと思いますが、大学の授業とはこのようなものです。
まとめ
突然、フーリエ級数展開を目の前に見せられると普通であればたじろいでしまうと思います。
しかし、フーリエ級数展開の意味がなんとなくでもわかれば、それがある種の魔法の数学的定義だということがわかると思います。
フーリエに関係するものはこれからどんどんと取り上げてゆきますので、それもあわせてお読みいただければ、フーリエ級数展開が持つその重要性がも身にしみてわかるはずです。
乞うご期待といったところです。


